Prenons deux exemples.
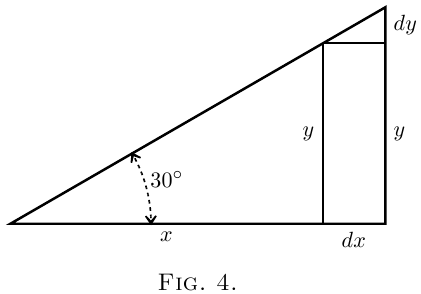
(1) Soient $x$ et $y$ représentant respectivement la base et la hauteur d'un triangle rectangle (Figure 4), où la pente du troisième coté est fixée à $30°$. Supposons que le triangle s'agrandisse tout en conservant l'angle que fait la pente avec l'horizontale. Dans un premier temps. Alors, lorsque la base grandit de $dx$ pour mesurer non plus $x$ mais $x + dx$, alors, la hauteur devient $y + dy$. Ici, faire croitre $x$ c'est aussi faire croître $y$. Le petit triangle de hauteur $dy$ et base $dx$ est similaire au triangle original; et il est évident que la valeur du ration entre $\dfrac{dy}{dx}$ et le même que celui entre $y$ et $x$ : $\dfrac{y}{x}$. Comme l'angle vaut $30°$ il sera vu que : \[ \frac{dy}{dx} = \frac{1}{1.73} . \]
(2) Soit $x$ dans la Figure 5, la distance horizontale entre le bas du mur et le bas de l'échelle, $AB$, est de longueur fixe (la longueur de l'échelle est constante) ; et soit $y$ la hauteur atteinte par l'échelle sur le mur. On voit clairement que $y$ dépend de $x$. C'est plutôt facile à voir, si on éloigne le point $A$ du mur, alors le haut de l'échelle $B$ va descendre un peu. Disons cela maintenant en langage mathématiques. Si on fait croitre $x$ de $dx$ : $x$ devient $x +dx$ alors $y$ sera diminué d'une petite quantité $dy$ donnant la nouvelle hauteur du point $B$ : $y - dy$; ce qui fait que quand $x$ est augmenté d'un petit peu, l'opération qui permet d'obtenir le $y$ est une soustraction d'un petit élément.
Oui, mais combien ? Supposons que l'échelle soit si longue que si l'extrémité inférieure $A$ est à $19$ pouces du mur l'extrémité supérieure $B$ a atteint à seulement $15$ pieds de hauteur. Maintenant, si vous deviez tirer sur l'extrémité inférieure à $1 $ de pouce de plus, de combien descendrait le haut de l'échelle? Mettez le tout en pouces : $x = 19$ pouces, $y = 180$ pouces. Maintenant on peut affirmer que l'incrément de $x$ que nous appelons $dx$, est de $1$ pouces : ou $x + dx = 20$ pouces. Soit la nouvelle distance entre le point $A$ et le bas du mur. De combien $y$ va-t-il diminuer? La nouvelle hauteur sera $y - dy$. Si on calcul la hauteur selon Euclide I. 47, alors nous pouvons facilement trouver la longueur de $dy$. En 2021 on dira plus facilement "Selon le théorème de Pythagore...". Commençons par calculer la longueur de l'échelle. Elle vaut :
\[
\sqrt{ (180)^2 + (19)^2 } = 181 \text{ pouces}.
\]
Clairement, on a alors la nouvelle hauteur $y - dy$ telle que :
\begin{align*}
(y - dy)^2 &= (181)^2 - (20)^2 = 32761 - 400 = 32361, \\
y - dy &= \sqrt{32361} = 179.89 \text{ pouces}.
\end{align*}
Maintenant $y$ vaut $180$, alors $dy$ vaut $180 - 179.89 = 0.11$ pouce. On voit maintenant qu'associer la valeur $1$ à $dx$ aura pour résultat une diminution de $y$ de $dy = 0.11$ pouces. Et le ration de $dy$ sur $dx$ sera alors :
\[
\frac{dy}{dx} = - \frac{0.11}{1}.
\]
Il est aussi assez facile de voir que, sauf dans une position particulière, $dy$ sera toujours différents de $dx$. Maintenant si on plonge un peu plus dans le calcul différentiel, on s'aperçoit que l'on chasse une chose curieuse, un simple ratio, à proprement parler, le rapport de la longueur $dy$ sur $dx$ quand tous les deux sont infiniment petits. Il faut noter que l'on peut trouver un tel ratio $\dfrac{dy}{dx}$ quand $y$ et $x$ sont dépendants l'un de l'autre, d'une manière ou d'une autre de manière à ce que dès que $x$ varie, $y$ varie aussi. Par exemple, dans le premier montré au dessus, si la base du triangle est agrandie, alors sa hauteur l'est aussi. Dans le second exemple, si le pied de l'échelle est éloigné du bas du mur, alors le haut de celle-ci descendra, de plus en plus vite plus $x$ deviendra grand. De ce cas, la relation entre $yxy$ et $x$ est parfaitement définie et peut être exprimée mathématiquement : $\dfrac{y}{x} = \tan 30°$
et $x^2 + y^2 = l^2$ (où $l$ est la longueur de l'échelle) respectivement, et $\dfrac{dy}{dx}$ a le même sens dans chaque cas. Considérons maintenant que $x$, comme précédemment, représente la distance entre le pied de l'échelle et le bas du mur, mais que maintenant $y$ représente autre chose. Au lieu de représenter la hauteur de l'échelle, admettons maintenant qu'il représente la longueur du mur, le nombre de briques qu'il contient ou encore le nombre d'année depuis qu'il fut construit. Alors, si on éloigne l'échelle du mur, que l'on modifie $x$ autrement dit, $y$ ne sera pas modifié; dans ce cas $\dfrac{dy}{dx}$ n'a aucun sens, quelque soit la manière dont on le regarde. Il n'est pas possible de trouver une expression pour $\dfrac{dy}{dx}$, ils ne sont pas en relation. quand on utilise les différentielles $dx$, $dy$, $dz$, etc., l'existence d'une relation entre les $x$, $y$, $z$, etc., est implicite et cette relation est appelée “fonction” de $x$, $y$, $z$, etc.; les deux expressions données en exemples ci-dessus, nommément
$\dfrac{y}{x} = \tan 30°$ et $x^2 + y^2 = l^2$, sont des fonctions de $x$ et $y$. Ces expressions contiennent implicitement les informations qui permettent d'exprimer (au moins localement et sous certaines conditions [Note 1]) $x$ en fonction de $y$ ou $y$ en fonction de $x$. Pour cette raison, ces fonctions que l'on appelle fonctions implicites en $x$ et en $y$; Dans certains cas il est possible d'exprimer comme ceci, respectivement :
\begin{align*}
y &= x \tan 30° \quad\text{ ou }\quad x = \frac{y}{\tan 30°} \\
\text{et}\;
y &= \sqrt{ l^2 - x^2} \quad\text{ ou }\quad x = \sqrt{ l^2 - y^2}.
\end{align*}
Ces deux dernières expressions, sont appellées fonctions explicites en $x$ ou $y$ (au contraire d'implicite). Pour cette raison ces fonctions sont appelées fonctions explicites : de par leur nature. Elles expriment soient les $x$ en termes de $y$ soit les $y$ en termes de $x$. Par exemple $x^2 + 3 = 2y - 7$ est une fonction implicite en $x$ et en $y$. Elle pourrait aussi être formulée : $y = \dfrac{x^2 + 10}{2}$ (fonction explicite de $x$) ou $x = \sqrt{2y - 10}$ (fonction explicite de $y$). Nous voyons donc qu'une fonction explicite en $x$, $y$, $z$, etc., est simplement quelque chose dont la valeur change quand $x$, $y$, $z$, etc., changent, soit une à la fois (fonctions de la variable réelle - NDT), soit toutes en même temps (fonctions à N variable - NDT). Avec toutes ces informations on peut dire qu'une fonction explicite est une variable dépendante, qui dépend d'autres quantités variables dans cette fonction, $x$, $y$, $z$, etc.; ces quantités variables sont des variables indépendantes car leurs valeurs ne sont pas déterminées par celles de la fonctions ou des autres variables. Par exemple, si $u = x^2 \sin \theta$, $x$ et $\theta$ sont les variables indépendantes, et $u$ est la variable dépendante. Parfois, la relation exacte entre plusieurs quantités $x$, $y$, $z$ est soit inconnue, soit n'a pas grand intérêt. Une fonction implique qu'il y a une relation entre ces variables. La seule chose connue est qu'il existe une relation entre les variables, de telles sorte qu'en modifiant l'une ou l'autre des $x$, $y$, $z$, etc. on modifie la valeur de la fonction, mais que modifier l'une ou l'autre n'aura pas d'impact entre elles. L'existence d'une fonction en $x$, ou $y$ ou $z$ est donnée par la notation suivante : $F(x, y, z)$ pour les fonctions implicites où $x = F(y, z)$, $y = F(x, z)$ ou $z = F(x, y)$
(fonctions explicites). De temps en temps on utilise $f$ ou $\phi$ au lieu de $F$, ainsi on a $y = F(x)$, $y = f(x)$ et $y = \phi(x)$. Ces trois dernières fonctions veulent dire exactement la même chose, la valeur de $y$ dépend de celle de $x$, d'une manière qui n'est pas forcément précisée ou dont on a pas forcément besoin tout de suite. On appelle le ratio $\dfrac{dy}{dx}$ “le nombre dérivé (anciennement appelé coefficient différentiel) de $y$ par rapport à $x$. Nom scientifique assez solennel pour une chose aussi simple. Mais nous n'allons pas nous laisser nous effrayer par de tels termes quand les choses sont aussi simples. Au lieu d'être effrayés par de tels termes, il suffira de ne les prononcer au pire en serrant les dents mais avant tout en se rappelant que ce qui est signifié est un simple ratio : $\dfrac{dy}{dx}$. En algèbre ou arithmétique, lorsque l'on commence les mathématiques, on cherche souvent à savoir quelle est la valeur d'une quantité souvent appelée $x$ ou $y$; voir même à chercher les deux en même temps (systèmes d'équations par exemple). Ce que nous cherchons dorénavant, ne sont plus $x$ ou $y$, mais le ratio $\dfrac{dy}{dx}$ (dans le livre original, une image avec la chasse à court est utilisée et d'une part la traduire n'a pas grand intérêt, mais de plus on ne citera pas plus avant cette pratique sauvage). Le processus qui est de rechercher la valeur de $\dfrac{dy}{dx}$ s'appelle la “différentiation”, ou “dérivation”. Mais il faut se rappeler que ce qui est recherché c'est le ratio quand $dy$ et $dx$ sont petits de manière indéfinies. La vraie valeur de la différentielle, ou dérivée est donnée par la valeur du ratio quand $dy$ et $dx$ sont infiniment petits. Apprenons maintenant comment partir à la quête de $\dfrac{dy}{dx}$.
Il ne faut jamais tomber dans les erreurs enfantines comme penser que $dx$ signifie $d$ fois $x$. $d$ n'est pas un facteur mis signifie "un élément de", voir "un très petit élément de", ou plus prosaïquement "unpetit élément de ", quoi qu'il s'ensuive. Quand on lit $dx$ on dit "dé - iks". Dans le cas où vous, le lecteur êtes seul pour aborder ces sujets, sachez que tout simplement, ces coefficients différentiels se lisent comme suit. Le nombre dérivé $\dfrac{dy}{dx}$ est lu “dé-y sur dé-iks”. La différentielle seconde, que l'on renctontrera plus tard ressemble à ça : $\dfrac{d^2 y}{dx^2};$
qui est lu “dé-deux-i-grec sur dé-iks carré,”, ce qui signifie que l'opération de différentiation (ou dérivation) de $y$ par rapport à $x$ a été faite deux fois de suite. Un autre moyen d'indiquer d'une fonction a été dérivée (différentiée) existe à l'aide de l'apostrophe. Si on ajoute une apostrophe à une fonction cela signifie la déricvée première de la fonction par rapport à sa variable. Aini, si $y=F(x)$, ce qui veut dire que $y$ est une sorte de fonction non précisée de $x$ (voir here), nous pouvons alors écrire $F'(x)$ au lieu de $\dfrac{d\bigl(F(x)\bigr)}{dx}$ De la même manière $F''(x)$ signifiera que la fonction initiale $F(x)$ a été dérivée deux fois par rapport à $x$. 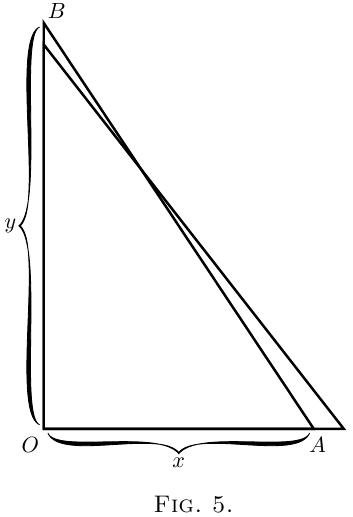
NOTES SUR LE CHAPITRE III.
Comment lire les différentielles.
Ainsi on a :
$\dfrac{du}{dt}$ qui est lue “dé-u sur dé-té.”
Note 1 : Le théorème des fonctions implicites est un sujet majeur dans les études mathématiques. J'ai vu des cours durer un semestre sur ce sujet. Quoi qu'il en soit ce sujet a été creusé depuis cet ouvrage et possède un formalisme et des théorèmes propres.
Next →
Main Page ↑