
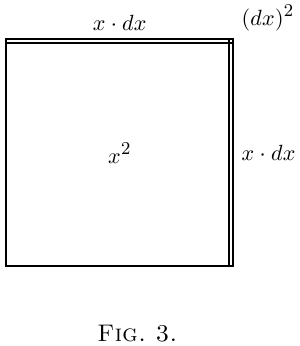
Géométriquement on pourrait décrire cela comme suit : Dessiner un carré (Figure 1) dont le coté est de longueur $x$. Maintenant supposons que l'on agrandisse le carré en ajoutant à chaque coté la longueur $dx$. Le carré ainsi agrandi est composé du carré original $x^2$, de deux rectangles en haut et à droite du carré, dont l'aire de chacun est donnée par $x · dx$ (ou si on ajoute les deux ensemble
$2x · dx$), et le petit carré en haut à droite qui vaut $(dx)^2$. Dans Figure 2 nous avons pris $dx$ comme une partie significative de $x$ –environ $\frac{1}{5}$. Mais supposons que nous ayons pris seulement $\frac{1}{100}$– environ l'épaisseur d'une ligne dessinée au stylo à encre. Alors le petit coin aura une aire de seulement $\frac{1}{10,000}$ de $x^2$, et sera pratiquement invisible. Clairement $(dx)^2$ est négligeable, mais seulement si on fait en sorte que l'incrément $dx$ soit suffisamment petit. Considérons une situation similaire.
Supposons qu'un millionnaire dise à son ou sa secrétaire : la semaine prochaine, je vous donnerai une petite fraction de tout l'argent que je recevrai. Supposons que le
secrétaire dise ensuite à son enfant : je te donnerai un
petite fraction de ce que je reçois. Supposons que la fraction
dans chaque cas soit $\frac{1}{100}$. Maintenant, si M. Millionnaire a reçu au cours de la semaine suivante £$1000$, la secrétaire recevrait £$10$ et l'enfant $2$ shillings. Dix livres sont une petite quantité par rapport à £$1000$; mais deux shillings est une minuscule quantité, comparativement, étant du second ordre par rapport aux £$1 000$. Mais qu'est-ce que cela changerait si la fraction étaient plus petite, au lieu d'être $\frac{1}{100}$, on aurait pris $\frac{1}{1000}$ ? La réponse est simple, pendant que M. Millionnaire a obtenu son £ $1000$, M. Secrétaire aurait obtenu seulement £$1$, et l'enfant moins d'un farthing ! Le très spirituel Dean Swift*
écrivit un jour: Un bœuf peut très bien être ennuyé par des mouches ordinaires -petites créatures du premier ordre de grandeur (petitesse). Mais il ne serait probablement pas dérangé par la mouche d'une mouche; cette toute petite mouche étant du second ordre de grandeur par rapport au bœuf . Cette mouche de mouche est négligeable. Même une nuée de mouches de mouche resteraient invisibles pour le bœuf . 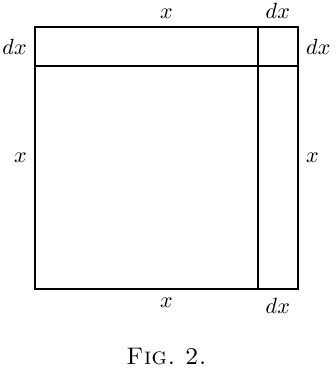
So, Nat'ralists observe, a Flea
Hath smaller Fleas that on him prey.
And these have smaller Fleas to bite 'em,
And so proceed ad infinitum."
Next →
Main Page ↑