Nous avons vu dans les équation précédentes le résultat sur $y$ lorsque l'on fait croître $x$ : nous avons répondu à la question qui dit de combien croit $y$ si on fait croitre $x$. On regarde toujours $x$ comme une quantité que l'on peut faire varier; et, on peut considérer que ces variation en $x$ sont la cause et les variations en $y$ l'effet. En d'autres termes, nous considérons la valeur de $y$ comme entièrement dépendante de celle de $x$. $x$ et $y$ sont toutes les deux des variables, mais $x$ est celle sur laquelle on peut réaliser des expressions et $y$ est en revanche la “variable dépendante.” Dans tout le chapitre précédent nous avons cherché à trouver dans quelle proportion varie $y$ quand on agit sur $x$, quel que soit $x$.
Notre prochaine étape consiste en l'analyse des effets de l'ajout d'une constante quand on différentie une fonction. Fonction dans laquelle on trouve une valeur qui ne change pas quelque soient les valeurs de $x$ et $y$.
Ajout de constantes.
[Note]NDT j'aurai pu écrire Constantes additives, mais si on respecte la volonté de l'auteur, employons des termes plus simples pour ne pas dire moins pompeux. [/Note]
Commençons par le simple cas ù on ajoute des constantes, comme ceci :
Soit :
\begin{align*}
y=x^3+5.
\end{align*}
Exactement comme auparavant, supposons que l'on fasse croitre $x$ en $x + dx$ avec $y$ qui vaudra $y+dy$.
Alors :
\begin{align*}
y + dy &= (x + dx)^3 + 5 \\
&= x^3 + 3x^2\, dx + 3x(dx)^2 + (dx)^3 + 5.
\end{align*}
En négligeant les termes d'ordre supérieurs à 1, on dit de grand ordre, on obtient :
\begin{align*}
y + dy &= x^3 + 3x^2·dx + 5. \\
\end{align*}
En soustrayant la fonction initiale : $y = x^3 + 5$, on obtient :
\begin{align*}
dy &= 3x^2\, dx. \\
\frac{dy}{dx} &= 3x^2.
\end{align*}
Le 5, la constante, a donc disparue. Il n'ajoute rien à la croissance de $x$ et ne rentre pas en ligne de compte dans le résultat du coefficient différentiel, la dérivée. Si on ajoute $7$ ou $700$ ou n'importe quel autre nombre, au lieu de $5$, il aurait disparu. So the $5$ has quite disappeared. It added nothing to the growth of $x$, and does not enter into the differential coefficient. If we had put $7$, or $700$, or any other number, instead of $5$, it would have disappeared. Donc si on prend n'importe quelle lettre $a$, $b$ ou $c$ pour représenter une constante, elle aurait simplement disparu par différentiation de la fonction.
Si la constante ajoutée est négative, comme $-5$ ou $-b$ elle disparait elle aussi.
Multiplication par une constante.
Prenons un exemple simple pour commencer :
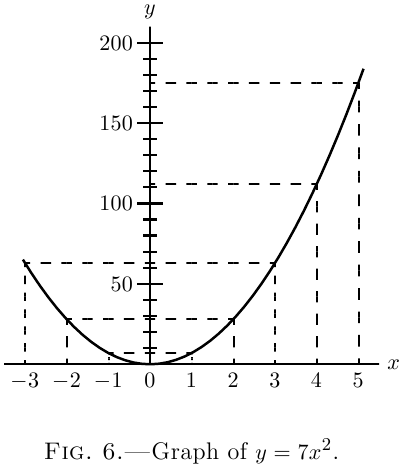
Soit $y = 7x^2$. En procédant comme nous avons fait auparavant : \begin{align*} y + dy &= 7(x+dx)^2 \\ &= 7\{x^2 + 2x·dx + (dx)^2\} \\ &= 7x^2 + 14x·dx + 7(dx)^2. \\ \end{align*} En soustrayant l'équation initiale $y = 7x^2$, et négligeant le dernier terme on obtient : \begin{align*} dy &= 14x·dx.\\ \frac{dy}{dx} &= 14x. \end{align*}
Illustrons cet exemple en travaillant sur le graphique de l'équation $y = 7x^2$ et $\dfrac{dy}{dx} = 14x$, en assignant à $x$ les valeurs suivantes $0$, $1$, $2$, $3$, etc., et de regarder quelle sont les valeurs correspondantes pour $y$ et $\dfrac{dy}{dx}$.
On présente ces valeurs dans le tableau suivant :
\begin{align*} \begin{array}{cccccccccc}\hline x & 0 & 1 & 2 & 3 & 4 & 5 & -1 & -2 & -3 \\ y & 0 & 7 & 28 & 63 & 112 & 175 & 7 & 28 & 63\\ \dfrac{dy}{dx} & 0 & 14 & 28 & 42 & 56 & 70 & -14& -28& -42\\ \hline \end{array} \end{align*}
On trace maintenant les courbes à l'aide de ces valeurs, dans une échelle adéquate, pour obtenir ces deux courbes, Fig. 6 et Fig. 6a.
Comparez attentivement les deux courbes et vérifiez que la valeur en $y$ de la dérivée de la fonction $\dfrac{dy}{dx}$ Fig. 6a,représente la pente de la courbe initiale, (Voir ici à propos de la pente des courbes. ) Figure 6, à la valeur correspondante de $x$. A gauche de l'origine, où pente de la courbe est négative (on lit de gauche à droite)les ordonnées correspondantes de la dérivée sont négatives.
Maintenant si on revient arrière en regardant ici, nous devrions nous apercevoir que dériver la simple fonction $x^2$ donne $2x$. Par conséquent, le coefficient différentiel de $7x^2$ vaut $7$ fois celui de $x^2$. Si nous avions pris $8x^2$, le coefficient différentiel aurait été huit fois plus grand que celui de $x^2$. Si nous posons $y = ax^2$, nous devrions obtenir : \[ \frac{dy}{dx} = a × 2x. \]
Et si nous avions commencé avec $y = ax^n$, nous aurions eu $\dfrac{dy}{dx} = a×nx^{n-1}$. Donc n'importe quelle multiplication par une constante fait qu'elle réapparait quand on a dérivé notre fonction. Et ce qui est vrai pour la multiplication l'est également pour la division : si dans l'exemple précédent on prend comme constante $\frac{1}{7}$ au lieu de $7$ nous aurions obtenu la même $\frac{1}{7}$ qui resterait après avoir dérivé la fonction.
D'autres exemples. Les exemples suivants, entièrement corrigés en détail vous permettront de maîtriser le processus de dérivation (différentiation) appliqués à ces fonction exprimées de manière algébriques et vous permettra de travailler par vous-même les exemples donnés à la fin de ce chapitre.
(1) Dériver $y = \dfrac{x^5}{7} - \dfrac{3}{5}$.
$\dfrac{3}{5}$ est une constante additive et disparait (voir ici).
On peut écrire directement : \[ \frac{dy}{dx} = \frac{1}{7} × 5 × x^{5-1}, \\ \] ou; \[ \frac{dy}{dx} = \frac{5}{7} x^4. \]
(2) Dériver $y = a\sqrt{x} - \dfrac{1}{2}\sqrt{a}$.
Le terme $\dfrac{1}{2}\sqrt{a}$ disparait, comme constante additive ; et comme $a\sqrt{x}$, dans forme naturelle peut être écrite $ax^{\frac{1}{2}}$, nous avons : \[ \frac{dy}{dx} = a × \frac{1}{2} × x^{\frac{1}{2}-1} = \frac{a}{2} × x^{-\frac{1}{2}}, \\ \] ou; \[ \frac{dy}{dx} = \frac{a}{2\sqrt{x}}. \]
(3) Si $ay + bx = by - ax + (x+y)\sqrt{a^2 - b^2}$,trouver la dérivée de $y$ selon $x$.
Cette expression nécessite de savoir une ou deux autres petites choses an plus de ce qui a été vu jusque ici; toutefois il est toujours intéressant de simplifier les expressions sur lesquelles on peut tomber.
Premièrement nous devons transformer cette expression pour en obtenir une de la forme $y = {}$, où dans ${}$ on trouve une expression qui dépend de $x$.
L'expression peut être écrite : \[ (a-b)y + (a + b)x = (x+y) \sqrt{a^2 - b^2}. \]
En mettant au carré on obtient : \[ (a-b)^2 y^2 + (a + b)^2 x^2 + 2(a+b)(a-b)xy = (x^2+y^2+2xy)(a^2-b^2), \] qui se simplifie en : \begin{align*} (a-b)^2y^2 + (a+b)^2 x^2 &= x^2(a^2 - b^2) + y^2(a^2 - b^2); \\ \end{align*} ou; \begin{align*} [(a-b)^2 - (a^2 - b^2)]y^2 &= [(a^2 - b^2) - (a+b)^2]x^2, \\ \end{align*} ce qui donne : \begin{align*} 2b(b-a)y^2 &= -2b(b+a)x^2; \end{align*} donc : \[ y = \sqrt{\frac{a+b}{a-b}} x \quad\text{and}\quad \frac{dy}{dx} = \sqrt{\frac{a+b}{a-b}}. \]
(4) Le volume d'un cylindre de rayon $r$ et hauteur $h$ est donné par la formule : $V = \pi r^2 h$. Trouver le taux de variation du volume quand le rayon vaut $r = 5.5$ in. et $h=20$ in. Si $r = h$, trouver les les dimensions du cylindre tel que si on change de $1$ in. le rayon cela cause une augmentation de $400$ cub. in. en volume.
Le taux de variation de $V$ selon $r$ est : \[ \frac{dV}{dr} = 2 \pi r h. \]
Si $r = 5.5$ in. et $h=20$ in. $\frac{dV}{dr} = 2 \pi r h$ vaut $690.8$. Cela signifie qu'un changement de $1$ pouce cause un changement de volume de $690.8$ cub. inch. Ce qui peut être facilement vérifié. Prenons les volumes correspondants aux rayons $r=5$ et $r=6$, soient $1570$ et $2260.8$ cub. inch. respectivement. Et comme : $2260.8 - 1570 = 690.8$ le résultat est bien conforme.
De plus, si : \[ r=h,\quad \dfrac{dV}{dr} = 2\pi r^2 = 400\quad \text{et}\quad r = h = \sqrt{\dfrac{400}{2\pi}} = 7.98 \text{in}. \]
(5) La valeur $\theta$ du pyromètre de Féry (instrument servant à mesurer les hautes températures) donne latempérature en Centigrades $t$ d'un corsp observé, grâce à la relation suivante : \[ \dfrac{\theta}{\theta_1} = \left(\dfrac{t}{t_1}\right)^4, \] où $\theta_1$ est une température de référence de 'objet observé dans une milieu à température connue $t_1$.
Comparer la sensibilité du pyromètre aux températures $800°$C., $1000°$C., $1200°$C., sachant que on lit sur le pyromètre la valeur $25$ quand la température valait $1000°$C.
la sensibilité est le taux de variation du résultat lu selon la température, s'exprime $\dfrac{d\theta}{dt}$. La formule peut s'écrire : \[ \theta = \dfrac{\theta_1}{t_1^4} t^4 = \dfrac{25t^4}{1000^4}, \] Et nous avons : \[ \dfrac{d\theta}{dt} = \dfrac{100t^3}{1000^4} = \dfrac{t^3}{10,000,000,000}. \]
Quand $t=800$, $1000$ and $1200$, on obtient $\dfrac{d\theta}{dt} = 0.0512$, $0.1$ and $0.1728$ respectivement.
La sensibilité double entre $800°$ et $1000°$, et grandit de trois quart à $1200°$.
Dériver ce qui suit: [2] (1) $y = ax^3 + 6$. (2) $y = 13x^{\frac{3}{2}} - c$.
(3) $y = 12x^{\frac{1}{2}} + c^{\frac{1}{2}}$. (4) $y = c^{\frac{1}{2}} x^{\frac{1}{2}}$.
(5) $u = \dfrac{az^n - 1}{c}$.
(6) $y = 1.18t^2 + 22.4$.
Construisez vous des exemples par vous-même et faites-vous la main sur la différentiation des fonctions.
(7) Si $l_t$ et $l_0$ représentent la longueur d'une tige de fer à une température $t°$ C. et $0°$ C. respectivement, alors $l_t = l_0(1 + 0.000012t)$. Trouver le taux de variation de la longueur de la tige par degré Centigrade.
(8) On a pu observer que si $c$ représente la luminosité d'une lampe électrique, et $V$ le voltage, alors $c = aV^b$, où $a$ et $b$ sont des constantes.
Trouver le taux de changement de la luminosité selon le voltage et calculer le taux de variation (coefficient différentiel) par volt à $80$, $100$ et $120$ volts dans la d'une lampe ou $a = 0.5×10^{-10}$ et $b=6$.
(9) La fréquence de vibration $n$ d'une corde de diamètre $D$, longueur $L$ et de gravité spécifique $\sigma$, étirée avec une force $T$, est donnée par : \[ n = \dfrac{1}{DL} \sqrt{\dfrac{gT}{\pi\sigma}}. \]
Trouver le taux de changement de la fréquence quand $D$, $L$, $\sigma$ et $T$ varient chacun leur tour.
(10) La pression extérieure $P$ que peut supporter un tube avant rupture (écrasement sur lui-même, en anglais collapse exprime parfaitement l'idée NDT) est donnée par la formule : \[ P = \left(\dfrac{2E}{1-\sigma^2}\right) \dfrac{t^3}{D^3}, \] où $E$ et $\sigma$ sont des constantes, $t$ est l'épaisseur du tube et $D$ son diamètre. Cette formule est valide sous l'hypothèse que $4t$ est petit comparé par rapport à $D$.
Comparer le taux de variation de $P$ pour un petit changement d'épaisseur puis pour un faible changement de diamètre, séparément.
(11) Trouver, à l'aide des premiers principes le taux de variation selon que l'on fait varier le rayon :
(a ) - le périmètre du cercle de rayon $r$;
(b ) - la surface du cercle de rayon $r$;
(c ) - la surface latérale d'un cône de cote oblique $s = \sqrt{r^2+h^2}=l$;
(d ) - le volume d'un cône de rayon $r$ et de hauteur $h$;
(e ) - la surface d'une sphère de rayon $r$;
(f ) - le volume d'une sphère de rayon $r$.
(12) La longueur d'une barre de fer à température $T$ est donnée par la relation $L = l_t\bigl[1 + 0.000012(T-t)\bigr]$, où $l_t$ est la longueur à la température $t$. Trouver le taux de variation du diamètre $D$ d'un pneu en fer que l'on va tordre pour former une roue, quand la température $t$ varie.
(1) $\dfrac{dy}{dx} = 3ax^2$.
(2) $\dfrac{dy}{dx} = 13 × \frac{3}{2}x^{\frac{1}{2}}$.
(3) $\dfrac{dy}{dx} = 6x^{-\frac{1}{2}}$.
(4) $\dfrac{dy}{dx} = \dfrac{1}{2}c^{\frac{1}{2}} x^{-\frac{1}{2}}$.
(5) $\dfrac{du}{dz} = \dfrac{an}{c} z^{n-1}$.
(6) $\dfrac{dy}{dt} = 2.36t$.
(7) $\dfrac{dl_t}{dt} = 0.000012×l_0$.
(8) $\dfrac{dC}{dV} = abV^{b-1}$, $0.98$, $3.00$ and $7.47$ candle power per volt respectively.
(9) \[ \dfrac{dn}{dD} = -\dfrac{1}{LD^2} \sqrt{\dfrac{gT}{\pi \sigma}}, \dfrac{dn}{dL} = -\dfrac{1}{DL^2} \sqrt{\dfrac{gT}{\pi \sigma}}, \\ \dfrac{dn}{d \sigma} = -\dfrac{1}{2DL} \sqrt{\dfrac{gT}{\pi \sigma^3}}, \dfrac{dn}{dT} = \dfrac{1}{2DL} \sqrt{\dfrac{g}{\pi \sigma T}}. \]
(10) \[ \dfrac{\text{Rate of change of $P$ when $t$ varies}} {\text{Rate of change of $P$ when $D$ varies}} = - \dfrac{D}{t} \]
(11) $2\pi$, $2\pi r$, $\pi l$, $\frac{2}{3}\pi rh$, $8\pi r$, $4\pi r^2$.
(12) $\dfrac{dD}{dT} = \dfrac{0.000012l_t}{\pi}$.