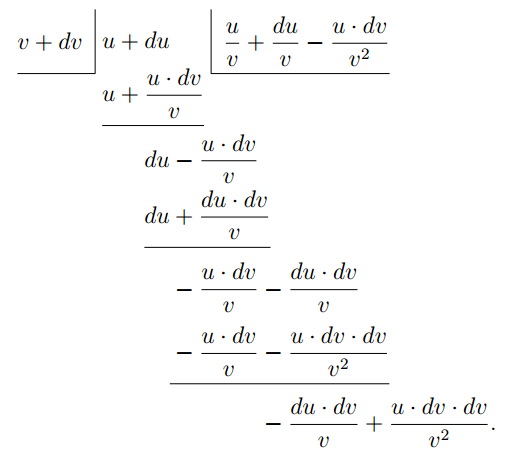
Nous avons jusqu'ici appris à dériver des expressions algébriques relativement simples comme $x^2 + c$ ou $ax^4$. Et nous allons maintenant considérer la somme de deux fonctions ou plus.
Par exemple soit : \[ y = (x^2+c) + (ax^4+b); \] Que vaudra sa dérivée $\dfrac{dy}{dx}$ ? Comment appréhender ces nouvelles expériences intellectuelles?
La réponse à cette question est relativement simple : les dériver l'une après l'autre. Comme ceci: \[ \dfrac{dy}{dx} = 2x + 4ax^3. (Ans.) \]
Si vous avez un doute sur la véracité de ce principe, essayez d'appliquer les premiers principes de calculs appliqués ici pour vous en convaincre.
soit $y = u+v$, où $u$ et $v$ sont deux fonctions de $x$, que l'on additionne pour donner $y$. Ainsi faire croître $x$ en $x+dx$ fera croître $y$ en $dy$. Et $u$ deviendra $u+du$ et $v$, $v +dv$.
Et nous devrions avoir :
$ y+dy = u+du + v+dv.$
En soustrayant l'original $y = u+v$, on obtient
$dy = du+dv, $
et en divisant par $dx$, on obtient:
$\dfrac{dy}{dx} = \dfrac{du}{dx} + \dfrac{dv}{dx}.$
Tout cela justifie la procédure que l'on vient de montrer : vous différentiez chaque fonction que vous ajoutez ensemble. Donc si on prend l'exemple du paragraphe précédent, en utilisant les expressions des deux fonctions on devrait avoir, en utilisant la notation montrée (dans le chapitre III), \begin{alignat*}{2} \frac{dy}{dx} & = \frac{d(x^2+c)}{dx} &&+ \frac{d(ax^4+b)}{dx} \\ & = 2x &&+ 4ax^3, \end{alignat*} exactement comme avant.
Si il y avait en fait trois fonctions de $x$, que l'on appellerait $u$, $v$ et $w$, de manière à ce que : \begin{align*} y &= u+v+w; \\ \end{align*} Alors : \begin{align*} \frac{dy}{dx} &= \frac{du}{dx} + \frac{dv}{dx} + \frac{dw}{dx}. \end{align*}
Comme pour l'addition, la soustraction en découle immédiatement. su une fonction $v$ a un signe négatif devant elle, sa différentielle le conservera. Ainsi par dérivation : \begin{align*} y &= u-v, \\ \end{align*} on devrait avoir : \begin{align*} \frac{dy}{dx} &= \frac{du}{dx} - \frac{dv}{dx}. \end{align*}
En revanche quand on arrive au produit, les choses ne sont plus si simples.
Supposons que nous devions dériver l'expression : \[ y = (x^2+c) × (ax^4+b), \] Comment faire? Le résultat ne sera certainement pas $2x × 4ax^3$; pour cela il est facile de voir que ni $c × ax^4$, ni $x^2 × b$, n'ont été pris en compte dans le produit.
a partir de là, on a deux manières de faire pour se mettre à travailler sur ce produit;
Première méthode. Faire la multiplication en premier puis dériver l'expression obtenue en dérivant.
Comme énoncé précédemment, multiplions $x^2 + c$ et $ax^4 + b$.
Cela donne $ax^6 + acx^4 + bx^2 + bc$.
Maintenant en dérivant on obtient : \[ \dfrac{dy}{dx} = 6ax^5 + 4acx^3 + 2bx. \]
Deuxième méthode. On réapplique les premiers principes vus pour dériver une fonction en considérant l'équation : \[ y = u × v; \] où $u$ et $v$ sont deux fonctions de la variable $x$. Alors, en faisant croître $x$ en $x + dx$, avec $y$ qui devient alors $y+dy$; De la même manière $u$ devient $u + du$ et $v$ devient $v +dv$. Nous devrions donc avoir : \begin{align*} y + dy &= (u + du) × (v + dv) \\ &= u · v + u · dv + v · du + du · dv. \end{align*}
Maintenant $du · dv$ est une petite quantité du second ordre de petitesse, il peut être négligé, pour donner : \[ y + dy = u · v + u · dv + v · du. \]
Puis, en soustrayant $y = u· v$, il reste : \[ dy = u · dv + v · du; \] et en divisant par $dx$ on obtient le résultat: \[ \dfrac{dy}{dx} = u\, \dfrac{dv}{dx} + v\, \dfrac{du}{dx}. \]
Tout ceci nous apprend que : Pour dériver un produit de deux fonctions, il faut multiplier chaque fonction par le coefficient différentiel de l'autre et ajouter les deux produits obtenus.
Pour se rappeler de comment dériver un produit, vous pouvez mémoriser les choses comme suit : Considérer que $u$ est une constante pendant que l'on dérive $v$; puis voir $v$ comme une constante et dériver $u$. La dérivée complète $\dfrac{dy}{dx}$ sera la somme de ces deux termes.
Maintenant que nous avons trouvé cette formule, appliquons là à notre exemple ci-dessus.
Nous voulons dériver ce produit : \[ (x^2 + c) × (ax^4 + b). \]
Posons $(x^2 + c) = u$; et $(ax^4 + b) = v$.
Alors, à l'aide de la formule générale que nous venons de trouver, nous pouvons écrire : \begin{alignat*}{2} \dfrac{dy}{dx} &= (x^2 + c)\, \frac{d(ax^4 + b)}{dx} &&+ (ax^4 + b)\, \frac{d(x^2 + c)}{dx} \\ &= (x^2 + c)\, 4ax^3 &&+ (ax^4 + b)\, 2x \\ &= 4ax^5 + 4acx^3 &&+ 2ax^5 + 2bx, \\ \dfrac{dy}{dx} &= 6ax^5 + 4acx^3 &&+ 2bx, \end{alignat*} Exactement comme précédemment.
Pour finir, voyons comment différencier les quotients.
Pensez à cet exemple : $y = \dfrac{bx^5 + c}{x^2 + a}$. Dans un tel cas, il n'est pas possible de calculer cette division, le numérateur $x^2 + a$ n'est pas un multiple du dénominateur $bx^5 + c$ et n'ont aucun facteur commun. Donc il n'y a rien d'autres à faire que d'appliquer les premières méthodes de dérivation vues au début et de trouver une formule. Donc soit : \[ y = \frac{u}{v}; \] où $u$ et $v$ sont deux fonctions différentes de la variable indépendante $x$. Alors, quand $x$ est modifié en $x+dx$, $y$ devient $y+dy$ et $u$ et $v$ deviennent $u+du$ et $v +dv$ respectivement. Ainsi : \[ y + dy = \dfrac{u + du}{v + dv}. \]
On réalise maintenant la division algébrique :
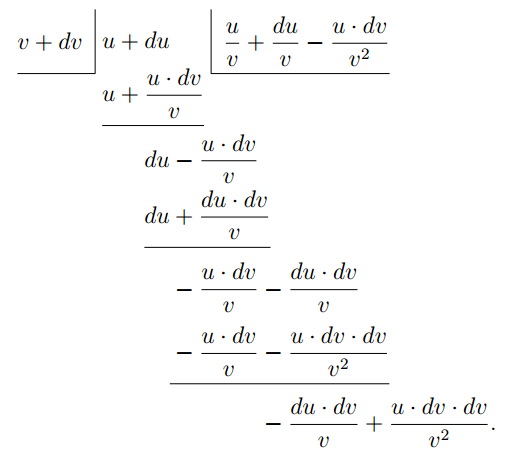
Les restes de la division sont du second ordre, ils peuvent donc être négligés, la division peut s'arrêter là. Les termes suivants de la division seront d'ordres supérieurs.
On a donc : \begin{align*} y + dy &= \dfrac{u}{v} + \dfrac{du}{v} - \dfrac{u· dv}{v^2}; \\ \end{align*} qui peut être réécrit : \begin{align*} &= \dfrac{u}{v} + \dfrac{v· du - u· dv}{v^2}. \\ \end{align*} Maintenant en soustrayant la fonction originale $y = \dfrac{u}{v}$, il reste : \begin{align*} dy &= \dfrac{v· du - u· dv}{v^2}; \\ \end{align*} d'où : \begin{align*} \dfrac{dy}{dx} &= \dfrac{v\, \dfrac{du}{dx} - u\, \dfrac{dv}{dx}}{v^2}. \end{align*}
Cette formule donne les instructions pour dériver un quotient de deux fonctions. On multiplie la fonction au dénominateur par la dérivée du numérateur, ce à quoi on soustraie la fonction au numérateur par la dérivée de celle au dénominateur, on divise le tout par le carré de la fonction au dénominateur.
En revenant à notre exemple $y = \dfrac{bx^5 + c}{x^2 + a}$, Ecrire : \begin{align*} bx^5 + c &= u; \\ \end{align*} et : \begin{align*} x^2 + a &= v. \end{align*}
Alors \begin{align*} \frac{dy}{dx} &= \frac{(x^2 + a)\, \dfrac{d(bx^5 + c)}{dx} - (bx^5 + c)\, \dfrac{d(x^2 + a)}{dx}}{(x^2 + a)^2} \\ &= \frac{(x^2 + a)(5bx^4) - (bx^5 + c)(2x)}{(x^2 + a)^2}, \\ \frac{dy}{dx} &= \frac{3bx^6 + 5abx^4 - 2cx}{(x^2 + a)^2}. \end{align*} Ce dernier quotient de fonctions est la dérivée recherchée.
Les calculs des dérivées de quotients peuvent être fastidieux, mais finalement ne sont pas difficile.
Quelques exemples corrigés dans le détails sont donnés dans la suite.
(1) Dériver $y = \dfrac{a}{b^2} x^3 - \dfrac{a^2}{b} x + \dfrac{a^2}{b^2}$.
Etant constante, la fraction $\dfrac{a^2}{b^2}$ disparait et nous avons : \[ \frac{dy}{dx} = \frac{a}{b^2} × 3 × x^{3-1} - \frac{a^2}{b} × 1 × x^{1-1}. \]
Mais $x^{1-1} = x^0 = 1$; donc on obtient : \[ \frac{dy}{dx} = \frac{3a}{b^2} x^2 - \frac{a^2}{b}. \]
(2) Dériver $y = 2a\sqrt{bx^3} - \dfrac{3b \sqrt[3]{a}}{x} - 2\sqrt{ab}$.
On peut écrire les termes en $x$ sous la forme suivante : \[ y = 2a\sqrt{b} x^{\frac{3}{2}} - 3b \sqrt[3]{a} x^{-1} - 2\sqrt{ab}. \]
Donc : \[ \frac{dy}{dx} = 2a\sqrt{b} × \tfrac{3}{2} × x^{\frac{3}{2}-1} - 3b\sqrt[3]{a} × (-1) × x^{-1-1}; \\ \] autrement écrit : \[ \frac{dy}{dx} = 3a\sqrt{bx} + \frac{3b\sqrt[3]{a}}{x^2}. \]
(3) Dériver $z = 1.8 \sqrt[3]{\dfrac{1}{\theta^2}} - \dfrac{4.4}{\sqrt[5]{\theta}} - 27°$.
Qui peut se réécrire : $z= 1.8\, \theta^{-\frac{2}{3}} - 4.4\, \theta^{-\frac{1}{5}} - 27°$.
Le terme $27°$ disparait et on obtient : \[ \frac{dz}{d\theta} = 1.8 × -\tfrac{2}{3} × \theta^{-\frac{2}{3}-1} - 4.4 × \left(-\tfrac{1}{5}\right)\theta^{-\frac{1}{5}-1}; \\ \text{ou}\;, \frac{dz}{d\theta} = -1.2\, \theta^{-\frac{5}{3}} + 0.88\, \theta^{-\frac{6}{5}}; \\ \text{ou encore,}\; \frac{dz}{d\theta} = \frac{0.88}{\sqrt[5]{\theta^6}} - \frac{1.2}{\sqrt[3]{\theta^5}}. \]
(4) Dériver $v = (3t^2 - 1.2 t + 1)^3$.
Une manière plus direct de calculer ce type de dérivées sera expliqué plus tard (voir ici); mais nous pouvons malgré tout calculer cette dérivée sans difficulté.
En développant le cube on obtient : \[ v = 27t^6 - 32.4t^5 + 39.96t^4 - 23.328t^3 + 13.32t^2 - 3.6t + 1; \] donc \[ \frac{dv}{dt} = 162t^5 - 162t^4 + 159.84t^3 - 69.984t^2 + 26.64t - 3.6. \]
(5) Dériver $y = (2x - 3)(x + 1)^2$. \begin{alignat*}{2} \frac{dy}{dx} &= (2x - 3)\, \frac{d\bigl[(x + 1)(x + 1)\bigr]}{dx} &&+ (x + 1)^2\, \frac{d(2x - 3)}{dx} \\ &= (2x - 3) \left[(x + 1)\, \frac{d(x + 1)}{dx}\right. &&+ \left.(x + 1)\, \frac{d(x + 1)}{dx}\right] \\ & &&+ (x + 1)^2\, \frac{d(2x - 3)}{dx} \\ &= 2(x + 1)\bigl[(2x - 3) + (x + 1)\bigr] &&= 2(x + 1)(3x - 2) \end{alignat*} Ou tout simplement en développant l'expression et dérivant terme à terme.
(6) Dériver $y = 0.5 x^3(x-3)$. \begin{align*} \frac{dy}{dx} &= 0.5\left[x^3 \frac{d(x-3)}{dx} + (x-3) \frac{d(x^3)}{dx}\right] \\ &= 0.5\left[x^3 + (x-3) × 3x^2\right] = 2x^3 - 4.5x^2. \end{align*}
Mêmes remarques que précédemment.
(7) Dériver $w = \left(\theta + \dfrac{1}{\theta}\right) \left(\sqrt{\theta} + \dfrac{1}{\sqrt{\theta}}\right)$.
Qui peut se réécrire : \begin{gather*} w = (\theta + \theta^{-1})(\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}}). \\ \begin{aligned} \frac{dw}{d\theta} &= (\theta + \theta^{-1}) \frac{d(\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}})}{d\theta} + (\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}}) \frac{d(\theta+\theta^{-1})}{d\theta} \\ &= (\theta + \theta^{-1})(\tfrac{1}{2}\theta^{-\frac{1}{2}} - \tfrac{1}{2}\theta^{-\frac{3}{2}}) + (\theta^{\frac{1}{2}} + \theta^{-\frac{1}{2}})(1 - \theta^{-2}) \\ &= \tfrac{1}{2}(\theta^{ \frac{1}{2}} + \theta^{-\frac{3}{2}} - \theta^{-\frac{1}{2}} - \theta^{-\frac{5}{2}}) + (\theta^{ \frac{1}{2}} + \theta^{-\frac{1}{2}} - \theta^{-\frac{3}{2}} - \theta^{-\frac{5}{2}}) \\ &= \tfrac{3}{2} \left(\sqrt{\theta} - \frac{1}{\sqrt{\theta^5}}\right) + \tfrac{1}{2} \left(\frac{1}{\sqrt{\theta}} - \frac{1}{\sqrt{\theta^3}}\right). \end{aligned} \end{gather*}
Encore une fois, on aurait pu obtenir le résultat en développant l'expression et en dérivant chaque terme. Mais ce n'est pas forcément possible à chaque fois. Par exemple voir ici, exemple 8, dans lequel la formule de dérivation d'un produit doit être utilisée.
(8) Dériver $y =\dfrac{a}{1 + a\sqrt{x} + a^2x}$. \begin{align*} \frac{dy}{dx} &= \frac{(1 + ax^{\frac{1}{2}} + a^2x) × 0 - a\dfrac{d(1 + ax^{\frac{1}{2}} + a^2x)}{dx}} {(1 + a\sqrt{x} + a^2x)^2} \\ &= - \frac{a(\frac{1}{2}ax^{-\frac{1}{2}} + a^2)} {(1 + ax^{\frac{1}{2}} + a^2x)^2}. \end{align*}
(9) Dériver $y = \dfrac{x^2}{x^2 + 1}$. \[ \dfrac{dy}{dx} = \dfrac{(x^2 + 1)\, 2x - x^2 × 2x}{(x^2 + 1)^2} = \dfrac{2x}{(x^2 + 1)^2}. \]
(10) Dériver $y = \dfrac{a + \sqrt{x}}{a - \sqrt{x}}$.
En mettant les termes en $x$ sous forme de puissance, $y = \dfrac{a + x^{\frac{1}{2}}}{a - x^{\frac{1}{2}}}$. \[ \frac{dy}{dx} = \frac{(a - x^{\frac{1}{2}})( \tfrac{1}{2} x^{-\frac{1}{2}}) - (a + x^{\frac{1}{2}})(-\tfrac{1}{2} x^{-\frac{1}{2}})} {(a - x^{\frac{1}{2}})^2} = \frac{ a - x^{\frac{1}{2}} + a + x^{\frac{1}{2}}} {2(a - x^{\frac{1}{2}})^2\, x^{\frac{1}{2}}}; \\ \] donc \[ \frac{dy}{dx} = \frac{a}{(a - \sqrt{x})^2\, \sqrt{x}}. \]
(11) Dériver
\begin{align*} \theta &= \frac{1 - a \sqrt[3]{t^2}}{1 + a \sqrt[2]{t^3}}. \\ \text{Now}\; \theta &= \frac{1 - at^{\frac{2}{3}}}{1 + at^{\frac{3}{2}}}. \end{align*} \begin{align*} \frac{d\theta}{dt} &= \frac{(1 + at^{\frac{3}{2}}) (-\tfrac{2}{3} at^{-\frac{1}{3}}) - (1 - at^{\frac{2}{3}}) × \tfrac{3}{2} at^{\frac{1}{2}}} {(1 + at^{\frac{3}{2}})^2} \\ &= \frac{5a^2 \sqrt[6]{t^7} - \dfrac{4a}{\sqrt[3]{t}} - 9a \sqrt[2]{t}} {6(1 + a \sqrt[2]{t^3})^2}. \end{align*}
(12) A traduire
(13) La pression absolue $P$ en atmosphère, de la vapeur saturée à température $t°$ C. est donnée par la formule de Dulong, par : $P = \left( \dfrac{40 + t}{140} \right)^5$ tant que $t$ reste au dessus de $80°$. Trouver le taux de variation de la pression pour une température de $100°$.
On développe le numérateur à l'aide de la formule du binôme de newton. Que l'on verra ici. \[ P = \frac{1}{140^5} (40^5 + 5×40^4 t + 10 × 40^3 t^2 + 10 × 40^2 t^3 + 5 × 40t^4 + t^5); \] Donc \begin{align*} \dfrac{dP}{dt} = &\dfrac{1}{537,824 × 10^5}\\ &(5 × 40^4 + 20 × 40^3 t + 30 × 40^2 t^2 + 20 × 40t^3 + 5t^4), \end{align*} Quand $t = 100°$ cela devient $0.036$ atmosphère par degré centigrade.
(a) $u = 1 + x + \dfrac{x^2}{1 × 2} + \dfrac{x^3}{1 × 2 × 3} + \dotsb$.
(b) $y = ax^2 + bx + c$. (c ) $y = (x + a)^2$.
(d) $y = (x + a)^3$.
(2) Si $w = at - \frac{1}{2}bt^2$, trouver $\dfrac{dw}{dt}$.
(3) Trouver le nombre dérivé de (on ne dit plus $\sqrt{-1}$ mais $i$): \[ y = (x + \sqrt{-1}) × (x - \sqrt{-1}). \]
(4) Dériver \[ y = (197x - 34x^2) × (7 + 22x - 83x^3). \]
(5) Si $x = (y + 3) × (y + 5)$, trouver $\dfrac{dx}{dy}$.
(6) Dériver $y = 1.3709x × (112.6 + 45.202x^2)$.
Trouver les différentielles des fonctions suivantes :
(7) $y = \dfrac{2x + 3}{3x + 2}$.
(8) $y = \dfrac{1 + x + 2x^2 + 3x^3}{1 + x + 2x^2}$.
(9) $y = \dfrac{ax + b}{cx + d}$.
(10) $y = \dfrac{x^n + a}{x^{-n} + b}$.
(11) La température $t$ du filament d'une lampe à incandescence est léie au courant qui passe dans la lampe selon cette relation : \[ C = a + bt + ct^2. \]
donner la formule liant la variation du courant avec celle de la température. (12) La formule suivante a été proposée pour exprimer la relation entre la résistance électrique $R$ d'un câble à température $t°C.$,et la résistance $R_0$ de ce même câble à $0°C.$, $a$, $b$, $c$ étant des constantes. \begin{align*} R &= R_0(1 + at + bt^2). \\ R &= R_0(1 + at + b\sqrt{t}). \\ R &= R_0(1 + at + bt^2)^{-1}. \end{align*}
Trouver le taux de variation de la résistance selon la variation de la température dan chaque formule.
(13) La force électromotrice observée $E$ de certains types de cellules varie avec la température $t$ selon la relation : \[ E = 1.4340 \bigl[1 - 0.000814(t-15) + 0.000007(t-15)^2\bigr] \text{ volts}. \]
Trouver le taux de variations de la force électromotrice par degré, à $15°$, $20°$ et $25°$.
(14) La force électromotrice nécessaire à créer et entretenir un arc électrique de longueur $l$ avec un courant d'intensité $i$ a été trouvée par Madame Ayrton : \[ E = a + bl + \frac{c + kl}{i}, \] où $a$, $b$, $c$, $k$ sont des constantes.
Trouver une expression pour la variation de la force électromotrice
(a) Selon la longueur de l'arc ;
(b) selon la force du courant.
(1) (a) $1 + x + \dfrac{x^2}{2} + \dfrac{x^3}{6} + \dfrac{x^4}{24} + \ldots$
(b) $2ax + b$.
(c ) $2x + 2a$.
(d) $3x^2 + 6ax + 3a^2$.
(2) $\dfrac{dw}{dt} = a - bt$.
(3) $\dfrac{dy}{dx} = 2x$.
(4) $14110x^4 - 65404x^3 - 2244x^2 + 8192x + 1379$.
(5) $\dfrac{dx}{dy} = 2y + 8$.
(6) $185.9022654x^2 + 154.36334$.
(7) $\dfrac{-5}{(3x + 2)^2}$.
(8) $\dfrac{6x^4 + 6x^3 + 9x^2}{(1 + x + 2x^2)^2}$.
(9) $\dfrac{ad - bc}{(cx + d)^2}$.
(10) $\dfrac{anx^{-n-1} + bnx^{n-1} + 2nx^{-1}}{(x^{-n} + b)^2}$.
(11) $b + 2ct$.
(12) $R_0(a + 2bt)$, $R_0 \left(a + \dfrac{b}{2\sqrt{t}}\right)$, $-\dfrac{R_0(a + 2bt)}{(1 + at + bt^2)^2}$ or $\dfrac{R^2 (a + 2bt)}{R_0}$.
(13) $1.4340(0.000014t - 0.001024)$, $-0.00117$, $-0.00107$, $-0.00097$.
(14) $\dfrac{dE}{dl} = b + \dfrac{k}{i}$, $\dfrac{dE}{di} = -\dfrac{c + kl}{i^2}$.