Les quaternions
Application des quaternions aux rotations - UP
Contexte et hypothèses
Avant de définir les rotations à l'aide des quaternions, on doit définir ce qu'est une rotation. Pour pouvoir l'implémenter en tant que quaternion.
Une rotation est entièrement et uniquement définie à l'aide d'un axe et d'un angle. L'axe est donné par un vecteur et l'angle par un scalaire, en général en radians. Une hypothèse supplémentaire nécessaire pour la simplicité des calculs est de choisir le vecteur de l'axe de rotation comme unitaire. Autrement, dit, lorsque vous définissez un axe de rotation, il faut que sa norme soit égale à $1$.
Rotation d'un élément de l'espace
Si on fait tourner une figure de l'espace, que fait on tourner? Les points caractéristiques de la figure. Si c'est un cube, alors on fait tourner chaque point de celui-ci. De la même manière pour une surface, même s'il existe des moyens plus rapides, que l'on évoquera par la suite. Si c'est une sphère, il suffit de faire tourner son centre et en connaissant son rayon, on trouve facilement l'image d'une sphère par une rotation dont l'axe ne passe pas par le centre de la sphère. Sinon, c'est trivial, l'image est elle-même.
Enoncé du problème
Donc, soit une rotation $\mathcal{R}_{\vec{u},\theta}$ d'axe donné par le vecteur $\vec{u}$ et d'angle $\theta$. L'objet à faire tourner est un point de l'espace. Si vous savez faire tourner un point, vous saurez faire tourner toute figure de l'espace, qu'elle soit définie par un, deux ou trois mille points. Donc le point $M$ de coordonnées $(x_{M};y_{M};z_{M})$. A ce point on associe naturellement le vecteur $\overrightarrow{OM}$, dont les coordonnées sont les mêmes que que le point $M$.
On va donc faire tourner le vecteur $\overrightarrow{OM}$ d'un angle $\theta$ par rapport à l'axe donné par le vecteur $\vec{u}$.
Point vu comme un quaternion
Première étape: transformer le vecteur à faire tourner en quaternion. Si on a $\overrightarrow{OM} = (x_{M};y_{M};z_{M})$ alors on peut définir le quaternion associé $q_{M}$:
$$
q_{M} = (0 ; x_{M};y_{M};z_{M}) = x_{M}.i + y_{M}.j + z_{M}.k
$$
Quaternion de la rotation
Deuxième étape, on traduit la rotation sous forme de quaternion. La rotation $\mathcal{R}_{\vec{u},\theta}$ est définie par son axe, lui même défini par le vecteur $\vec{u}$ et son d'angle $\theta$.
Alors le quaternion d'une rotation est donné par la formule suivante:
$$
q_\mathcal{R} = (cos\theta/2; u_{x}.sin\theta/2; u_{y}.sin\theta/2; u_{z}.sin\theta/2)
$$
Avec pour condition que $\vec{u}$ soit unitaire. $ u_{x}$, $ u_{y}$ et $ u_{z}$ sont ses composantes.
Si le vecteur de l'axe de rotation n'est pas unitaire, alors multiplier le quaternion par l'inverse de la norme du vecteur de l'axe et le quaternion sera unitaire. Et permettra de représenter une rotation.
Pour finir la construction de la rotation sous forme de quaternion, il faut maintenant prendre le conjugué du précédent quaternion, soit:
$$
q^{\star}_\mathcal{R} = (cos\theta/2; - u_{x}.sin\theta/2; - u_{y}.sin\theta/2; - u_{z}.sin\theta/2)
$$
On peut maintenant présenter la formule qui permet de calculer l'image d'un point par une rotation dans l'espace, à l'aide des quaternions. On pose: $\overrightarrow{OM^{'}} = (x_{M^{'}};y_{M^{'}};z_{M^{'}})$ l'image du point $M$ par la rotation, et son quaternion associé: $q_{M^{'}}$. Alors:
$$
q_{M^{'}} = q_\mathcal{R} . q_{M} . q^{\star}_\mathcal{R}
$$
Exemples d’application - UP
Voici un tableau contenant quelques quaternions correspondant à certaines rotations. Quelques
exemples peuvent permettre d’implémenter plus facilement ces éléments.
Considérons q un quaternion et ses composantes:
q = (a; b; c; d)
$$
\begin{align*}
\begin{array}{|c|c|c|c|c|} \hline
a & b & c & d & \text{Rotations résultantes} \\ \hline
1 & 0 & 0 & 0 & \text{Identité = rotation d'angle nul } \\ \hline
0 & 1 & 0 & 0 & \text{Rotation autour de l’axe des }x \\ \hline
0 & 0 & 1 & 0 & \text{Rotation autour de l’axe des $y$}, \\ \hline
0 & 0 & 0 & 1 & \text{Rotation autour de l’axe des $z$}, \\ \hline
\dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} & 0 & 0 & \text{Rotations de $\pi/2$ par rapport $\vec{i}$} \\ \hline
\dfrac{\sqrt{2}}{2} & 0 & \dfrac{\sqrt{2}}{2} & 0 & \text{Rotations de $\pi/2$ par rapport $\vec{j}$ } \\ \hline
\dfrac{\sqrt{2}}{2} & 0 & 0 & \dfrac{\sqrt{2}}{2} & \text{Rotations de $\pi/2$ par rapport $\vec{k}$ } \\ \hline
\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} & 0 & 0 & \text{Rotations de $-\pi/2$ par rapport $\vec{i}$ } \\ \hline
\dfrac{\sqrt{2}}{2} & 0 & -\dfrac{\sqrt{2}}{2} & 0 & \text{Rotations de $-\pi/2$ par rapport $\vec{j}$ } \\ \hline
\dfrac{\sqrt{2}}{2} & 0 & 0 & -\dfrac{\sqrt{2}}{2} & \text{Rotations de $-\pi/2$ par rapport $\vec{k}$ } \\
\hline
\end{array}
\end{align*}
$$
Soit $M$ le point de coordonnées $(1;0;1)$. On veut le faire tourner d'un quart de tour ($\pi/2$) par rapport à l'axe des $z$, dans le sens positif. L'axe de rotation est donné par le vecteur unitaire $\vec{u} = (0;0;1)$On a donc:
$$
q_{M} = i + k
$$
et
$$
q_\mathcal{R} = (cos\pi/4; 0 ; 0 ; sin\pi/4) = \dfrac{\sqrt{2}}{2}+ \dfrac{\sqrt{2}}{2}.k
$$
$$
q^{\star}_\mathcal{R} = (cos\pi/4; 0 ; 0 ; sin\pi/4) = \dfrac{\sqrt{2}}{2} - \dfrac{\sqrt{2}}{2}.k
$$
Donc:
$$
q_{M^{'}} = (\dfrac{\sqrt{2}}{2}+ \dfrac{\sqrt{2}}{2}.k) . (i + k) . (\dfrac{\sqrt{2}}{2} - \dfrac{\sqrt{2}}{2}.k)\\
= \dfrac{1}{2} (1+k).(i+k).(1-k)\\
= \dfrac{1}{2} (i+k+ki+k^{2}).(1-k)\\
= \dfrac{1}{2} (i+k+j-1).(1-k)\\
= \dfrac{1}{2} (i+k+j-1-ik-k^{2}-jk+k)\\
= \dfrac{1}{2} (i+k+j-1+j+1-i+k)\\
= \dfrac{1}{2} (2j+2k)\\
= j+k\\
$$
Par une rotation d'un quart de tour par rapport à l'axe des $z$, la rotation du point $M = (1 ; 0 ; 1)$ est bien le point $M' = (0 ; 1 ; 1)$:
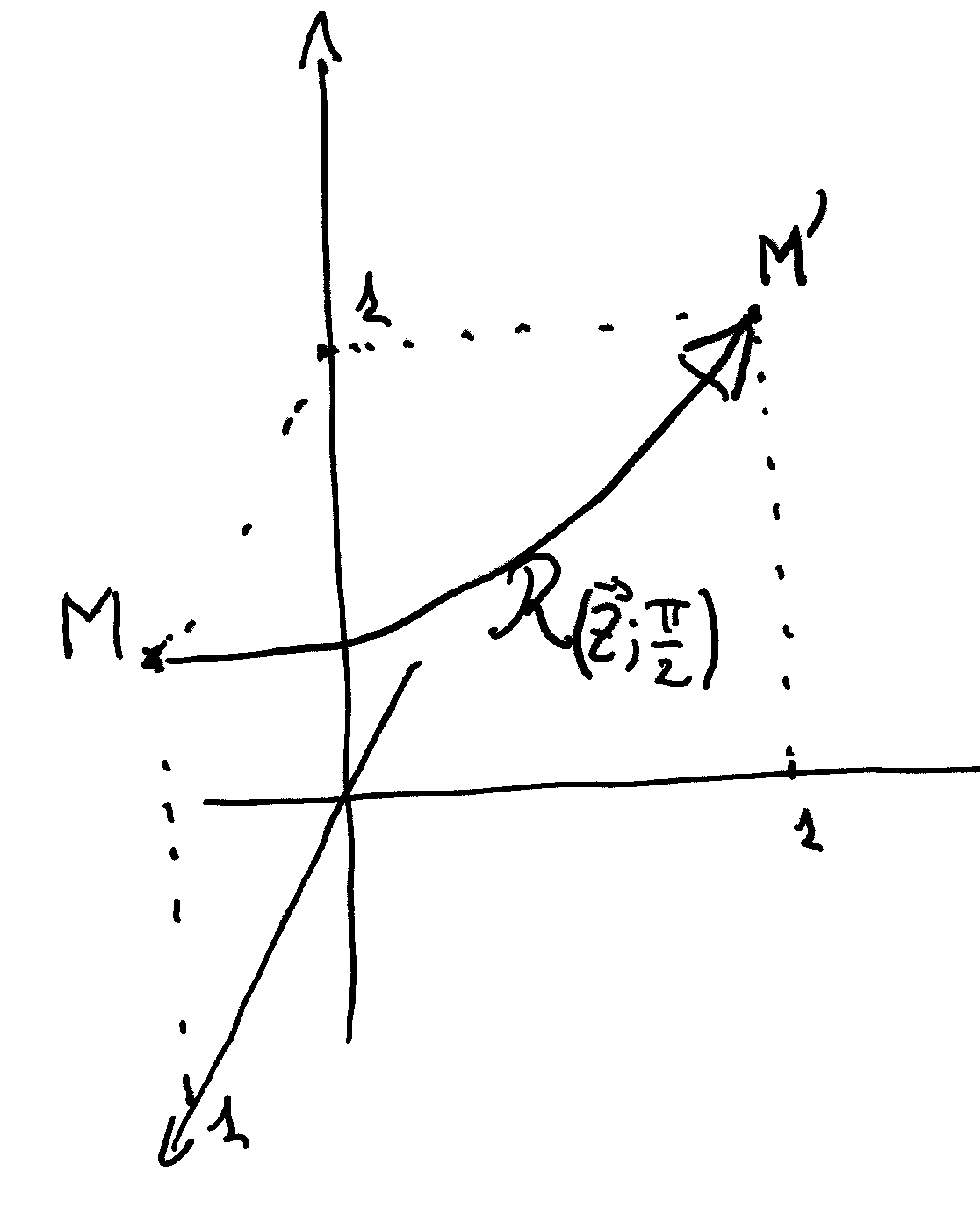 [!h]
[!h]
Exercices d'application - UP
Produit d'un quaternion et de son conjugué
Soit :
\[
p = 1 + \mathbf{i} + \mathbf{j} - \mathbf{k}, \quad
\overline{p} = 1 - \mathbf{i} - \mathbf{j} + \mathbf{k}
\]
1. Norme
\[
\|p\| = \sqrt{1^2 + 1^2 + 1^2 + (-1)^2} = 2
\]
2. Normalisation
\[
p_n = \tfrac{1}{2}(1 + \mathbf{i} + \mathbf{j} - \mathbf{k}), \quad
\overline{p_n} = \tfrac{1}{2}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k})
\]
3. Produit développé
\[
p_n \overline{p_n} = \tfrac{1}{4}(1 + \mathbf{i} + \mathbf{j} - \mathbf{k})(1 - \mathbf{i} - \mathbf{j} + \mathbf{k})
\]
\[
\begin{aligned}
(1 + \mathbf{i} + \mathbf{j} - \mathbf{k})(1 - \mathbf{i} - \mathbf{j} + \mathbf{k})
&= 1(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) \\[3pt]
&\quad + \mathbf{i}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) \\[3pt]
&\quad + \mathbf{j}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) \\[3pt]
&\quad - \mathbf{k}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k})
\end{aligned}
\]
Détail des termes :
\[
\begin{aligned}
1(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) &= 1 - \mathbf{i} - \mathbf{j} + \mathbf{k} \\[6pt]
\mathbf{i}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) &= 1 + \mathbf{i} - \mathbf{j} - \mathbf{k} \\[6pt]
\mathbf{j}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) &= 1 + \mathbf{i} + \mathbf{j} + \mathbf{k} \\[6pt]
-\mathbf{k}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) &= -1 - \mathbf{i} + \mathbf{j} - \mathbf{k}
\end{aligned}
\]
4. Somme des quatre lignes
\[
(1 - \mathbf{i} - \mathbf{j} + \mathbf{k})
+ (1 + \mathbf{i} - \mathbf{j} - \mathbf{k})
+ (1 + \mathbf{i} + \mathbf{j} + \mathbf{k})
+ (-1 - \mathbf{i} + \mathbf{j} - \mathbf{k})
\]
\[
\Rightarrow \text{partie réelle } = 2, \quad \text{partie imaginaire } = 0
\]
\[
(1 + \mathbf{i} + \mathbf{j} - \mathbf{k})(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}) = 4
\]
5. Facteur de normalisation
\[
p_n \overline{p_n} = \tfrac{1}{4} \times 4 = 1
\]
Résultat final
\[
\boxed{
p_n = \tfrac{1}{2}(1 + \mathbf{i} + \mathbf{j} - \mathbf{k}), \quad
\overline{p_n} = \tfrac{1}{2}(1 - \mathbf{i} - \mathbf{j} + \mathbf{k}), \quad
p_n \overline{p_n} = 1
}
\]
Ainsi, \(p_n\) est un quaternion unitaire, représentant une rotation pure.
Limites de ces pages - UP
Cette page web ne se veut pas comme être la référence théorique sur les quaternions. Son objectif est uniquement de permettre de les appréhender d'un point de vue appliqué pour permettre leur utilisation en programmation 3D. La théorie des quaternions est vaste et touche diverses domaines des mathématiques, de l'algèbre linéaire, bilinéaire, sesquilinéaire, algèbre pur, Analyse complexe.
Page suivante →
Retour à l'accueil →
 [!h]
[!h]
 [!h]
[!h]