Rappel des notions de collège

... Ordres de grandeurs, notation scientifique, les différents types de nombres. On commencera par une bête noire: les fractions

Les fractions — définitions et opérations

En langage courant une fraction est une partie de... "Est-ce que tu as fini de trier toutes les données?" où une réponse peut être "Seulement une fraction" pour dire que ce n'est pas la totalité. Plus précisément, dire j'en ai fait la moitié, un quart, presque un tiers, signifie qu'une fraction de ce qui devait être fait l'a été. Ces fractions sont le coté intuitifs de ce concept, dont la description est très précise en maths. Comme nous allons le voir ci-dessous.

Plus généralement une fraction est une division: le chiffre placé au dessus du trait de fraction est divisé par celui en dessous.

Définition
Une fraction est un nombre de la forme :
$ \dfrac{a}{b} $, avec $ b \neq 0 $
où $ a $ est le numérateur et $ b $ le dénominateur.
Exemple: $ \dfrac{1}{3} $,$ \dfrac{5}{4} $,$ \dfrac{75}{100} $,$ \dfrac{22}{7} $,$ \dfrac{1}{10} $, ...
On peut écrire tout nombre entier comme une fraction : $ 17 = \dfrac{17}{1} $ ; n'importe quel nombre divisé par $1$ est égal à lui même. Exercice:
Ecrire les fractions suivantes au sens mathématiques:
Un fruit sur deux est pourri ;
Dix sept éléphants sur trente deux sont mécontent ;

Fraction d'un nombre
On peut toujours voir une fraction comme le produit d'un nombre de l'inverse d'un autre. Si par exemple on a la fraction $ \dfrac{a}{b} $, elle peut être écrite :

$$ \dfrac{a}{b} = a \times \dfrac{1}{b} $$

On peut voir la division comme une multiplication d'un nombre, $a$ par un autre: $\dfrac{1}{b}$. On a toujours une fraction, le $\dfrac{1}{b}$. En revanche le voir comme un produit tel qu'écrit au dessus est correct mathématiquement.

Visuellement
Donner la fracion représentée dans ces images suivantes :
Schéma 1 :
1/2
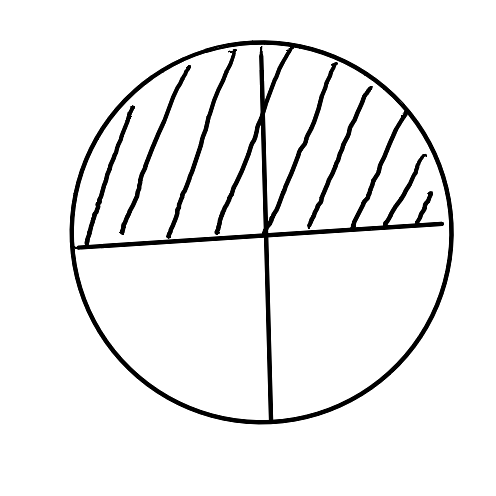
Schéma 2 :
3/4
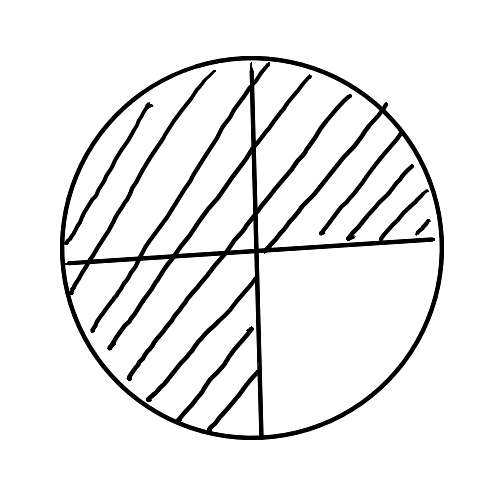
Schéma 3 :
3/8
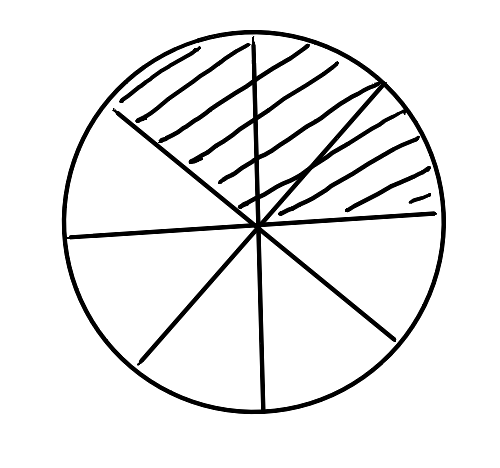
Schéma 4 :
5/8
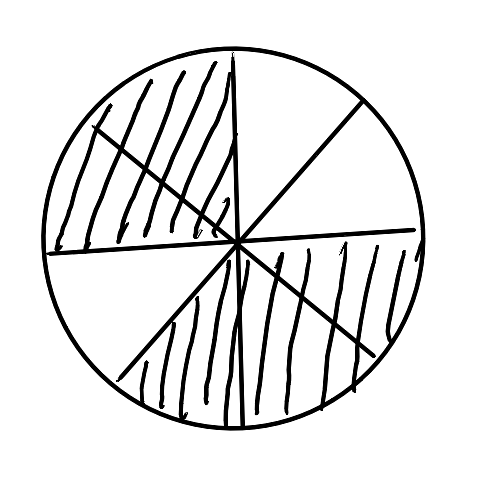
Schéma 5 :
1/8
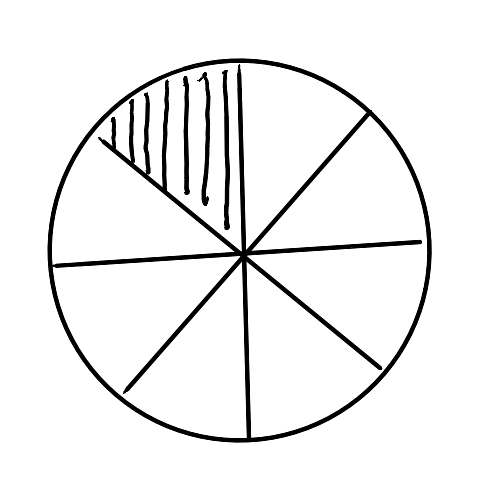
Schéma 6 :
7/8

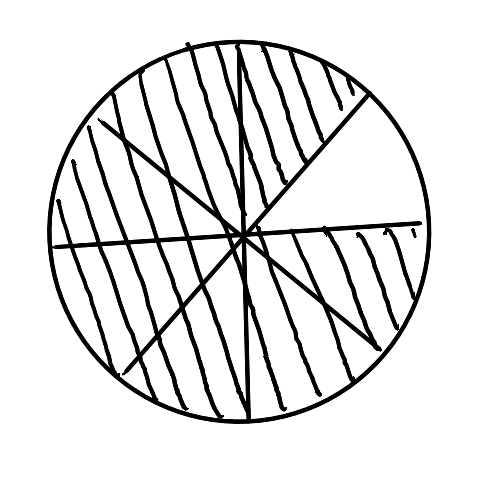
Solution : au passage de la souris sur chaque image!

Égalité de fractions
Une même fraction peut être écrite de plusieurs manière, tout en ayant la même valeur. Par exemple $1/2$ et $2/4$ représentent la même fraction.

On a la formule suivante :
$$ \dfrac{a}{b} = \dfrac{c}{d} \iff a \times d = b \times c $$

Exemple: a-t-on $ \dfrac{3}{2} = \dfrac{9}{6} $? On regarde les produits $2 \times 9$ et $3 \times 6$. Comme les deux valent $18$, ces fractions sont égales.
On pourra voir aussi que si les numérateurs et dénominateurs ont même proportionnalité, alors les fractions sont égales.

Les fractions suivantes sont elles égales?
$\dfrac{3}{4}$ et $\dfrac{18}{24}$
$\dfrac{7}{3}$ et $\dfrac{9}{21}$
$\dfrac{4}{5}$ et $\dfrac{80}{100}$
$\dfrac{75}{3}$ et $25$
$\dfrac{17}{11}$ et $\dfrac{187}{121}$
$\dfrac{1}{2}$ et $\dfrac{733}{1466}$

Pour la solution, faites la division sur une calculatrice pour confirmer!

Simplification
La simplification des fractions est appris très tôt et
On divise le numérateur et le dénominateur par un même nombre non nul :
$ \dfrac{a}{b} = \dfrac{a \div k}{b \div k} $, avec $ k \neq 0 $

Fraction égale (amplification)
$ \dfrac{a}{b} = \dfrac{a \times k}{b \times k} $

Addition de fractions de même dénominateur
$ \dfrac{a}{b} + \dfrac{c}{b} = \dfrac{a + c}{b} $

Addition de fractions de dénominateurs différents
$ \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd} $

Soustraction
$ \dfrac{a}{b} - \dfrac{c}{d} = \dfrac{ad - bc}{bd} $

Multiplication
$ \dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{a \times c}{b \times d} $

Division
$ \dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \times \dfrac{d}{c} = \dfrac{a \times d}{b \times c} $

Inverse d'une fraction
$ \left( \dfrac{a}{b} \right)^{-1} = \dfrac{b}{a} $, avec $ a \neq 0 $

Puissance d'une fraction
$ \left( \dfrac{a}{b} \right)^n = \dfrac{a^n}{b^n} $

Comparaison de fractions
$ \dfrac{a}{b} > \dfrac{c}{d} \iff ad > bc $ (si $ b,d > 0 $)

Transformation en nombre décimal
$ \dfrac{a}{b} = a \div b $

Les puissances — définitions et propriétés

Définition
Pour tout nombre réel $ a $ et tout entier naturel $ n \geq 1 $ :
$ a^n = \underbrace{a \times a \times \dots \times a}_{n\ \text{facteurs}} $

Cas particuliers
$ a^1 = a $, $ a^0 = 1 $ (si $ a \neq 0 $), $ a^{-n} = \dfrac{1}{a^n} $

Produit de puissances de même base
$ a^m \times a^n = a^{m+n} $

Quotient de puissances de même base
$ \dfrac{a^m}{a^n} = a^{m-n} $, avec $ a \neq 0 $

Puissance d'une puissance
$ (a^m)^n = a^{m \times n} $

Puissance d'un produit
$ (a \times b)^n = a^n \times b^n $

Puissance d'un quotient
$ \left( \dfrac{a}{b} \right)^n = \dfrac{a^n}{b^n} $, avec $ b \neq 0 $

Puissance d'un nombre négatif
Si $ n $ est pair, $ (-a)^n = a^n $
Si $ n $ est impair, $ (-a)^n = -a^n $

Écriture scientifique
Tout nombre réel $ x $ peut s'écrire :
$ x = a \times 10^n $, avec $ 1 \leq |a| < 10 $ et $ n \in \mathbb{Z} $

Racine carrée et puissance fractionnaire
$ \sqrt{a} = a^{\frac{1}{2}} $, plus généralement :
$ \sqrt[n]{a} = a^{\frac{1}{n}} $

Puissance à exposant rationnel
$ a^{\frac{m}{n}} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m $, avec $ a > 0 $

Proportionnalité, pourcentages, échelles

La proportionnalité permet de mettre en relation des quantités pour que si on a connaît la donnée pour une, on connaît celle de l'autre. Cette phrasue assez abstraite peut être accompagnée d'un exemple concret: Au marché, on veut acheter des bananes. Elles valent deux euros le kilos. Sachant cela il est facile de savoir le pris à payer pour trois kilos. Comme elles coûtent deux euros le kilos, on en veut trois, alors le prix total sera de trois3 kilos fois deux euros.

Expressions littérales, calculs algébriques simples

Géométrie

Eléments de géométrie tels que les droites, cercles, tangentes, angles, médiatrices, médianes,

Triangles, parallèles, perpendiculaires

Les différents types et leurs caractéristiques : quelconque, rectangle, scalène, isocèle, équilatéral, isocèle rectangle et leurs droites caractéristiques : hauteur, médiane et médiatrice

Angles, cercles, médiatrices, bissectrices

Théorèmes (Pythagore, Thalès), similitude

Transformations : symétrie, rotation, translation, agrandissement

Fonctions

Notion de variable, représentation graphique simple

Fonctions linéaires et affines

Statistiques et probabilités

Comprendre la notion d'échantillons et les grands principes des stats. Les quatre chapitres traitant de ces sujets sont à voir d'un point de vue plus culture générale que véritablement opérationnellement.

Le collège ou la structuration logique

Fractions, puissances et autres outils ...